The building and construction sectors are responsible for 39% of global greenhouse gas emissions, but they are among the largest consumers of energy. If all indicators show that demand would be exponential in the future. Decarbonization and reduction of energy consumption in buildings are urgent for environmental preservation and resilience to extreme temperature increases. This article aims to present environmentally friendly bio-sourced insulation as a more sustainable circular economy strategy. However, we present the results of thermal and mechanical characterization of plaster samples with the addition of typha fibers in different proportions. Thus, after having carried out the mechanical traction and compression tests by the press, a thermophysical characterization by the asymmetric hot plane method allowed us to have the conductivity and thermal effusivity of the different samples of plaster binder with 0%, 5%, 10%, 15% and 20% in typha. With these data, we modeled the heat transfer phenomena in a flat wall based on plaster-typha. A numerical resolution of the heat equation by the finite difference method is applied to this model along one dimension. After simulating the calculation code, the results obtained made it possible to know the evolution of the temperature as a function of time and the depth of the wall. In addition, the influence of the exchange coefficients was highlighted on both sides, in order to know the optimal thermal insulation thickness of each sample.
| Published in | Advances in Materials (Volume 14, Issue 2) |
| DOI | 10.11648/j.am.20251402.11 |
| Page(s) | 36-45 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Characterization, Thermomechanics, Conductivity, Effusivity, Traction, Compression, Numerical Modeling, Typha-plaster and Exchange Coefficients
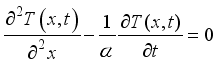 (1)
(1) 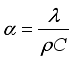 (2)
(2) 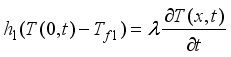
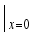 (3)
(3) 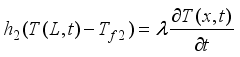
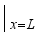 (4)
(4) 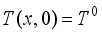 (5)
(5) 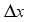 in the direction (ox) and that of time
in the direction (ox) and that of time 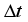 . The steps are constant.
. The steps are constant. 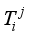 est la température au nœud i à la date j.
est la température au nœud i à la date j. 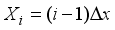 (6)
(6) 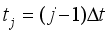 (7)
(7) 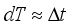 (8)
(8) 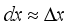 (9)
(9) 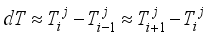 (10)
(10) 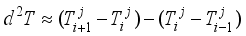 (11)
(11) 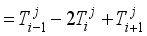
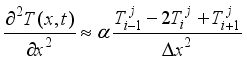 (12)
(12) 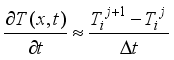 (13)
(13) 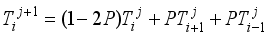 (14)
(14) 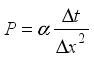 (15)
(15) 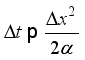 (16)
(16) 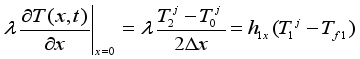 (17)
(17) 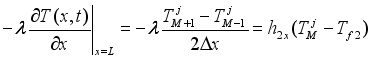 (18)
(18) 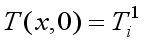 (19)
(19) 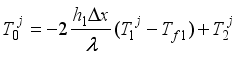 (20)
(20) 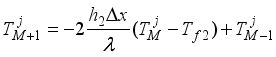 (21)
(21) 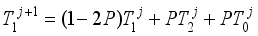 (22)
(22) 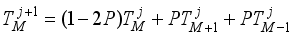 (23)
(23) 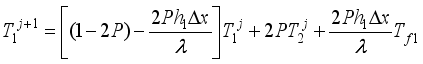 (24)
(24) 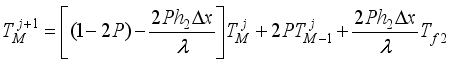 (25)
(25) 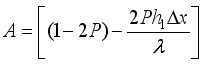 (26)
(26) 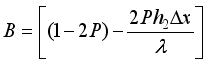 (27)
(27) 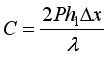 (28)
(28) 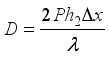 (29)
(29) 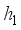 et
et 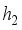 are constants hence the boundary conditions at point i=1 and i=M taking into account the parameters
are constants hence the boundary conditions at point i=1 and i=M taking into account the parameters 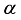 , A, B, C et D.
, A, B, C et D. 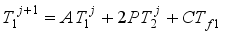 (30)
(30) 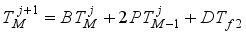 (31)
(31) 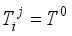 (32)
(32) 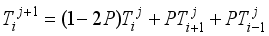 (33)
(33) 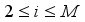 et
et 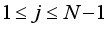
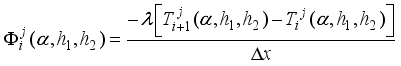 (34)
(34) 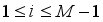 et
et 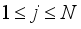
Sample Typha plaster (0%, 5%, 10%, 15% et 20%) | E0 | E5 | E10 | E15 | E20 |
|---|---|---|---|---|---|
Mass of dry samples in g | 274,67 | 224,29 | 183,59 | 135,33 | 131,9 |
Thermal conductivity in W/m.K | 0,6795 | 0,1743 | 0,1554 | 0,1378 | 0,0652 |
Thermal effusivity in J/..K. | 1022,4 | 560,9213 | 486,3481 | 447,8512 | 276,132 |
Thermal diffusivity | 4,4171 | 9,65586 | 1,02096 | 9,4674 | 5,57522 |
Density kg/ | 1373,35 | 1121,45 | 917,95 | 676,65 | 659,5 |
Mass Typha Plaster percentage | E0 | E5 | E10 | E15 | E20 | ||
|---|---|---|---|---|---|---|---|
Traction | Force en KN | 1,855 | 1,845 | 1,466 | 1,126 | 0,632 | |
Pressure in MPa | 0,412 | 0,410 | 0,326 | 0,250 | 0,141 | ||
Compression | C1 | Force en KN | 17,372 | 8,836 | 7,556 | 6,991 | 3,152 |
Pressure in MPa | 0,772 | 0,393 | 0,336 | 0,311 | 0,140 | ||
C2 | Force in KN | 17,749 | 10,282 | 7,891 | 6,912 | 3,965 | |
Pressure in MPa | 0,789 | 0,457 | 0,339 | 0,307 | 0,176 | ||
| Force en KN | 17,5605 | 9,559 | 7,7235 | 6,9515 | 3,5585 | |
Pression en MPa | 0,7805 | 0,425 | 0,3375 | 0,309 | 0,158 | ||
Masse in Kg | 320,05 | 279,30 | 257,15 | 198,97 | 135 | ||
Density Kg/ | 1250,195 | 1091,016 | 1004,492 | 777,226 | 527,344 | ||
K | Kelvin |
| [1] | Global Alliance for Buildings and Construction, «“2020 Global State of Buildings and Construction Report”». |
| [2] | Zheng Lu, Michael Hauschild, Lisbeth M. Ottosen, Teklit Gebregiorgis Ambaye, Pierluigi Zerbino, Davide Aloini, Ana T. Lima, « Climate mitigation potential of biobased insulation materials: A comprehensive review and categorization », Journal of Cleaner Production, volume 470, August 2024, pp. 143356, |
| [3] | Muralikrishnan Alagarsamy, P Pitchipoo, Senthil Kumar, « Comprehensive characterization of spathe fibres extracted from Cocos nucifera: physical, chemical, mechanical, thermal, and acoustic properties for insulation applications», Mater. Res. Express, volume 11, July 2024, pp. 075503. |
| [4] | Lin Chen, Mingyu Yang, Zhonghao Chen, Zhuolin Xie, Lepeng Huang, Ahmed I. Osman, Mohamed Farghali, Malindu Sandanayake, Engui Liu, Yong Han Ahn, Ala’a H. Al-Muhtaseb, David W. Rooney, Pow-Seng Yap, «Conversion of waste into sustainable construction materials: A review of recent developments and prospects», Materials Today Sustainability, volume 27,25 July 2024, pp. 100930, |
| [5] | Sophie Trachte, Dorothée Stiernon, « Balanced choice of thermal insulation during renovation. How to meet energy performance requirements while limiting the overall environmental impact and promoting the circularity of materials,” lieuxdits#24, December 2023, pp. 14-21. |
| [6] | Aguerata Kabore, Claudiane M. Ouellet-Plamondon, « Improved insulation with fibres in heavy cob for building walls », Industrial Crops & Products, volume 215, May 2024, pp. 118626, |
| [7] | Henri W. Hounkpatina, Victorin K. Chegnimonhanb, Hagninou E. V. Donnoua, Guy H. Hounguè, Basile B. Kounouhewa, « Thermal characterisation of insulation panels based on vegetable typha domengensis and starch », scientific African, volume 21, 2023, pp. e01786, |
| [8] | Thibaut Lecompte, «Hemp in the buildings of tomorrow: advantages, constraints and challenges”, Annales de Bretagne et des Pays de l’Ouest, online January 4, 2023. |
| [9] | Ahmed Alami, Lala Rajaoarisoa, Nicolas Dujardin, Ali Benouar, Khacem Kaddouri, Khedidja Benouis and Mohammed-Hichem Benzaama, « Artificial Intelligence Approach for Bio-Based Materials’ Characterization and Explanation », Buildings, volume, June 2024, pp. 1602, |
| [10] | Basim Abu-Jdayila, Abdel-Hamid Mourad, Waseem Hittini, Muzamil Hassand, Suhaib Hameedi, « Traditional, state-of-the-art and renewable thermal building insulation materials: An overview », Construction and Building Materials, volume 214, 2019, pp. 709–735, |
| [11] | M. S. Ould Brahim, S. Tamba, M. Sarr, A. Diène, I. Diagne, F. Niang et G. Sissoko, «Evolution of the overall thermal exchange coefficients of kapok-plaster and tow-plaster materials in dynamic frequency regime”, Revue des Energies Renouvelables, Vol. 14, N°2, 2011, pp. 203 – 210. |
| [12] | J. C. Damfeu, P. Meukama and Y. Jannot, « Modelling and measuring of the thermal properties of insulating vegetable fibers by the asymmetrical hot plate method and the radial flux method: kapok, coconut, groundnut shell fiber and rattan », Thermochimica Acta, volume 630, 2016, pp. 64-77, |
| [13] | Younouss Dieye, Vincent Sambou, Mactar Faye, Ababacar Thiama, Mamadou Adj et Dorothe Azilinon, « Thermo-mechanical characterization of a building material based on Typha Australis », Journal of Building Engineering volume 9, 2017, pp. 142-146, |
| [14] | Ibrahima Diaw, Mactar Faye, Stéphane Hans, Frederic Sallet and Vincent Sambou, «Valorization of the Recovered Lime in Cement-Typha Concretes: Thermal and Mechanical Behavior», InterSol 2022, LNICST, volume 449, February 2023, pp. 267–276 76, |
| [15] | El Hadji Abdoul Aziz CISSE, Papa Touty Traore, Alphousseyni GHABO, Mor Ndiaye, Issa Diagne, «Thermomechanical characterization of laterite matrix reinforced with typha material for thermal insulation in building », Materials Sciences and Applications, volume 15, 2024, pp. 450-463, |
| [16] | Harouna Bal, Yves Jannot, Salif Gaye, Frank Demeurie, «Measurement and modelisation of the thermal conductivity of a wet composite porous medium: Laterite based bricks with millet waste additive», Construction and Building Materials volume 41, January 2013, pp. 586–593, |
| [17] | Nadia Benmansour, Boudjemaa Agoudjil, Abdelkader Gherabli, Abdelhak Kareche, Aberrahim Boudenne, «Thermal and mechanical performance of natural mortar reinforced with date palm fibers for use as insulating materials in building», Energy and Buildings volume 81, June 2014, pp. 98–104, |
| [18] | Sibiath O. G. OSSENI, Berléo D. APOVO, Clément AHOUANNOU, Emile A. SANYA et Yves JANNOT, «Thermal characterization of cement mortars doped with coconut fibers by the asymmetric hot plane method at a temperature measurement», Afrique SCIENCE, volume 12, n°6, 2016, pp. 119 – 129. |
| [19] | Harouna Bal, Yves Jannot, Nathan Quenette, Alain Chenu, Salif Gaye, «Water content dependence of the porosity, density and thermal capacity of laterite-based bricks with millet waste additive», Construction and Building Materials, volume 31, January 2012, pp. 144–150, |
| [20] | Yoann Brouard, Naima Belayachi, Dashnor Hoxha, Narayanaswami Ranganathan, Stéphane Méo, «Mechanical and hygrothermal behavior of clay – Sunflower (Helianthus annuus) and rape straw (Brassica napus) plaster bio-composites for building insulation», Construction and Building Materials, volume 161, 2018, pp. 196–207. |
| [21] | A. Laborel-Préneron, J-E. Aubert, C. Magniont, A. Bertron, «Influence of straw content on the mechanical and thermal properties of bio-based earth composites», First International Conference on Bio-based Building Materials, 22 – 24 June 2015, Clermont-Ferrand, France. |
| [22] | Seydou FAYE, Papa Touty TRAORE and Babou DIONE, «Study in Transient Regime by Analytical Method of Heat Transfer through a Kapok-plaster Insulating Material has one Dimension: Influence of the Heat Exchange Coefficient», Journal of Scientific and Engineering Research, volume 8, n°9, 2021, pp. 199-206. |
| [23] | Mamadou Babacar Ndiaye, Ahmadou Diop, Seydou Faye, Youssou Traore and Gregoire Sissoko, «Study of a flat panel based on typha and clay in transient regime», Int. J. Adv. Res. Volume 8, n°12, December 2020, pp. 751-758. |
APA Style
Cisse, E. H. A. A., Traore, P. T., Faye, S., Dieng, M., Ndiaye, M., et al. (2025). Thermomechanical Characterization and Numerical Modeling of Thermal Transfer of Plaster-based Insulating Composite Materials with Gradual Typha Contents. Advances in Materials, 14(2), 36-45. https://doi.org/10.11648/j.am.20251402.11
ACS Style
Cisse, E. H. A. A.; Traore, P. T.; Faye, S.; Dieng, M.; Ndiaye, M., et al. Thermomechanical Characterization and Numerical Modeling of Thermal Transfer of Plaster-based Insulating Composite Materials with Gradual Typha Contents. Adv. Mater. 2025, 14(2), 36-45. doi: 10.11648/j.am.20251402.11
@article{10.11648/j.am.20251402.11,
author = {El Hadji Abdoul Aziz Cisse and Papa Touty Traore and Seydou Faye and Moussa Dieng and Mor Ndiaye and Issa Diagne},
title = {Thermomechanical Characterization and Numerical Modeling of Thermal Transfer of Plaster-based Insulating Composite Materials with Gradual Typha Contents
},
journal = {Advances in Materials},
volume = {14},
number = {2},
pages = {36-45},
doi = {10.11648/j.am.20251402.11},
url = {https://doi.org/10.11648/j.am.20251402.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.am.20251402.11},
abstract = {The building and construction sectors are responsible for 39% of global greenhouse gas emissions, but they are among the largest consumers of energy. If all indicators show that demand would be exponential in the future. Decarbonization and reduction of energy consumption in buildings are urgent for environmental preservation and resilience to extreme temperature increases. This article aims to present environmentally friendly bio-sourced insulation as a more sustainable circular economy strategy. However, we present the results of thermal and mechanical characterization of plaster samples with the addition of typha fibers in different proportions. Thus, after having carried out the mechanical traction and compression tests by the press, a thermophysical characterization by the asymmetric hot plane method allowed us to have the conductivity and thermal effusivity of the different samples of plaster binder with 0%, 5%, 10%, 15% and 20% in typha. With these data, we modeled the heat transfer phenomena in a flat wall based on plaster-typha. A numerical resolution of the heat equation by the finite difference method is applied to this model along one dimension. After simulating the calculation code, the results obtained made it possible to know the evolution of the temperature as a function of time and the depth of the wall. In addition, the influence of the exchange coefficients was highlighted on both sides, in order to know the optimal thermal insulation thickness of each sample.
},
year = {2025}
}
TY - JOUR T1 - Thermomechanical Characterization and Numerical Modeling of Thermal Transfer of Plaster-based Insulating Composite Materials with Gradual Typha Contents AU - El Hadji Abdoul Aziz Cisse AU - Papa Touty Traore AU - Seydou Faye AU - Moussa Dieng AU - Mor Ndiaye AU - Issa Diagne Y1 - 2025/06/16 PY - 2025 N1 - https://doi.org/10.11648/j.am.20251402.11 DO - 10.11648/j.am.20251402.11 T2 - Advances in Materials JF - Advances in Materials JO - Advances in Materials SP - 36 EP - 45 PB - Science Publishing Group SN - 2327-252X UR - https://doi.org/10.11648/j.am.20251402.11 AB - The building and construction sectors are responsible for 39% of global greenhouse gas emissions, but they are among the largest consumers of energy. If all indicators show that demand would be exponential in the future. Decarbonization and reduction of energy consumption in buildings are urgent for environmental preservation and resilience to extreme temperature increases. This article aims to present environmentally friendly bio-sourced insulation as a more sustainable circular economy strategy. However, we present the results of thermal and mechanical characterization of plaster samples with the addition of typha fibers in different proportions. Thus, after having carried out the mechanical traction and compression tests by the press, a thermophysical characterization by the asymmetric hot plane method allowed us to have the conductivity and thermal effusivity of the different samples of plaster binder with 0%, 5%, 10%, 15% and 20% in typha. With these data, we modeled the heat transfer phenomena in a flat wall based on plaster-typha. A numerical resolution of the heat equation by the finite difference method is applied to this model along one dimension. After simulating the calculation code, the results obtained made it possible to know the evolution of the temperature as a function of time and the depth of the wall. In addition, the influence of the exchange coefficients was highlighted on both sides, in order to know the optimal thermal insulation thickness of each sample. VL - 14 IS - 2 ER -